Il problema dei tre corpi: esplorare e comprendere l'Universo

Scienza Di Stefania Bergo. Il problema dei tre corpi, portato all'attenzione dei più dalla trilogia di fantascienza di Cixin e dalla serie Netflix omonima, è un problema di meccanica classica che continua a sfidare e affascinare gli scienziati di tutto il mondo. Le sue applicazioni pratiche sono molteplici e ci permettono di guidare le nostre missioni spaziali alla scoperta dello spazio e di comprendere il comportamento dell'Universo.

Il problema dei tre corpi è stato portato all'attenzione dei più da una serie TV uscita per Netflix questo mese. La serie, per ora solo alla prima stagione, è ispirata alla trilogia fantascientifica Memoria del passato della Terra del 2006 – Il problema dei tre corpi, La materia del cosmo e Nella quarta dimensione – dello scrittore cinese Liu Cixin.
Il primo libro dell'opera si ispira a una classe di problemi di meccanica classica della dinamica dei corpi celesti. Si tratterebbe di trovare le soluzioni di un sistema di tre corpi soggetti alla reciproca interazione gravitazionale, appunto, per determinarne, date la massa, la posizione e la velocità iniziali, l'evoluzione nel tempo della posizione e della velocità future di ogni singolo pianeta all'interno del sistema stesso.
Ma un sistema formato da tre corpi sottoposti alla reciproca interazione gravitazionale non è descrivibile da equazioni con soluzioni esatte. Non è sufficiente applicare la Legge di gravitazione universale elaborata da Isaac Newton nel XVII secolo per prevedere i movimenti dei corpi.

La legge di gravitazione universale descrive, a livello teorico formale, i movimenti di pianeti, stelle e altri corpi celesti, partendo dal caso di due masse che interagiscono reciprocamente tra loro.

Isaac Newton, infatti, dimostrò che due corpi di massa m₁ ed m₂ si attraggono con una forza direttamente proporzionale al prodotto delle loro masse e inversamente proporzionale al quadrato della distanza r tra essi, secondo una costante G.

F = G	m1 m2
	r2

Tuttavia, quando si tratta di tre o più corpi, le cose diventano molto più complicate.

Il problema dei tre corpi riguarda il movimento di tre corpi celesti soggetti solo alla reciproca forza di gravità.

Sebbene possa sembrare relativamente semplice, la dinamica di questo sistema è incredibilmente complessa e non può essere risolta analiticamente in modo esatto, tranne in casi molto specifici.
Il movimento di due corpi è descrivibile con precisione risolvendo le equazioni della legge di gravitazione universale. Tuttavia, aggiungendo un terzo corpo, il sistema diventa caotico e imprevedibile.
Perché questa complessità per l'introduzione di un solo corpo in più? Perché le possibili interazioni si moltiplicano, cambia il modo in cui ogni corpo reagisce agli altri due. I corpi possono influenzarsi reciprocamente in modi che sfidano la nostra intuizione, con risultati come orbite instabili, collisioni o addirittura fuga dal sistema verso lo spazio aperto – su questo gioca il primo romanzo della trilogia di Cixin, sul fatto che un pianeta in un Sistema Solare con tre soli risulterebbe in balia del caos e potrebbe finire su uno degli astri bruciando o venire sparato nello spazio siderale congelando.

Davanti a tale complessità, gli scienziati hanno sviluppato diversi approcci per studiare il problema dei tre corpi.

La soluzione generale delle equazioni dinamiche di un sistema a tre corpi non è chiusa, cioè è rappresentata da una serie infinita di termini. Si parla quindi di approssimazione e non di soluzione analitica, semmai di soluzione matematica: attarverso una serie di approsimazioni successive ci si avvicina sempre più alla soluzione senza raggiungerla mai. Nel 1912 il matematico finlandese-svedese Karl Frithiof Sundman, ad esempio, sviluppò una serie infinita convergente [1] che offre una soluzione al problema dei tre corpi. Ma si tratta di una soluzione troppo lenta, cioè ottenere una precisione adeguata nei calcoli richiede un numero molto elevato di termini – siamo nell'ordine di oltre 100 milioni di termini – per cui il metodo non è utilizzabile in pratica.

Uno dei metodi più comuni per risolvere il problema è l'utilizzo di simulazioni al computer utilizzando metodi approssimativi.

Ad esempio si utilizzano le serie di potenze o le perturbazioni per risolvere numericamente le equazioni del moto, al fine di ottenere una comprensione dell'evoluzione del sistema. Ma anche in questo caso si tratta di approsimazioni, le soluzioni hanno validità limitata nel tempo, dato che il comportamento del sistema, che è di tipo caotico, diverge in modo imprevedibile: le condizioni al contorno si evolvono in continuazione e le equazioni vanno risolte di nuovo ogni volta.

Soluzioni esplicite al problema dei tre corpi si possono trovare soltanto per casi particolari, semplificando il sistema.

Problemi semplificati sono stati studiati da molti matematici e fisici, tra cui Jean Sylvain Bailly, Henri Poincaré e Tullio Levi-Civita.
In particolare, si parla di problema dei tre corpi ristretto, risolvendo il problema dei tre corpi a partire da quello dei due corpi introducendo una piccola modifica: la semplificazione consiste nel considerare la massa di uno dei tre corpi trascurabile rispetto agli altri due e di studiare il suo moto nel campo di forze generato dalle masse più grandi, considerando che l'introduzione della terza massa non lo possa perturbare.

Il problema dei tre corpi ristretto.

Nel caso di tre corpi in moto nello spazio – m₁, m₂ ed m₃ – di cui uno abbia massa trascurabile rispetto agli altri due – supponiamo m₃ –, si studia il campo gravitazionale creato dal sistema di due corpi m₁ ed m₂ considerando che su di essi agisca solo la mutua forza di gravità. Con la legge di gravitazione universale si determinano le linee del campo gravitazionale su cui si muoverà m₃ una volta introdotta nel sistema, considerando che, data la massa irrisoria rispetto alle altre due, non lo perturbi affatto.

In tale campo gravitazionale, esistono cinque posizioni di equilibrio detti punti di Lagrange.

Cioè punti in cui m₃ rimane in equilibrio, come se su di essa non agissero forze, "ferma" rispetto al sistema m₁ – m₂ stesso. La distribuzione di questi punti, indicati con L1, L2, L3, L4 e L5, è visibile nell'immagine seguente. Tre di questi punti – L1, L2 e L3 – si trovano su una retta che congiunge i due corpi di massa maggiore m₁ ed m₂. Questi punti rappresentano delle posizioni di equilibrio instabile. I restanti due punti – L4 e L5 – sono punti di equilibrio stabile e sono collocati sull'orbita del pianeta di massa intermedia – m₂ – attorno all'altro – m₁ –, formando un angolo di 60° con la retta che congiunge m₁ e m₂, in modo tale che il segmento immaginario che congiunge m₁ e m₂ sia la base di due triangoli equilateri di vertici nei punti L4 ed L5. [2]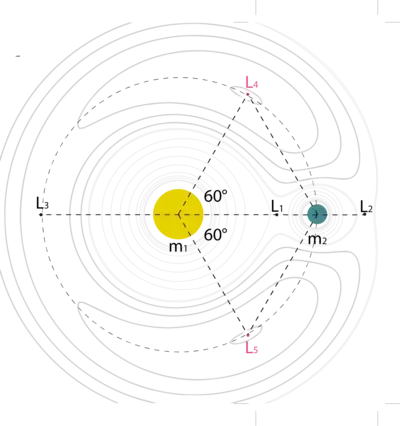

Il problema dei tre corpi semplificato ha profonde implicazioni nella comprensione dell'Universo stesso: ad esempio permette di mettere in orbita i satelliti, di prevedere le rotte delle comete o spiegare il moto degli asteroidi Troiani di Giove.

Lo studio del problema dei tre corpi è fondamentale per la progettazione di missioni spaziali, dove è essenziale comprendere il movimento di satelliti artificiali o telescopi spaziali soggetti all'attrazione gravitazionale di più corpi celesti. Ci aiuta anche a capire fenomeni naturali come le interazioni tra stelle in sistemi stellari multipli, le orbite dei pianeti extrasolari e persino la stabilità a lungo termine del nostro stesso Sistema Solare.
Considerando la figura qui sopra, si possono distinguere i punti di equilibrio di Lagrange dovuti alla reciproca interazione delle due masse più grandi – m₁ e m₂ – mentre le linee in grigio chiaro rappresentano praticamente le possibili orbite del terzo corpo in movimento nel campo gravitazionale del sistema.

Sonde spaziali, telescopi e i punti di equilibrio di Lagrange del sistema Terra-Sole di interesse per la nostra esplorazione spaziale.

Supponiamo che le due masse più grandi siano il Sole e la Terra e che la terza massa sia una sonda per l'esplorazione spaziale.
Analizzando la conformazione dei punti di equilibrio di Lagrange, la posizione migliore per una sonda terrestre che voglia studiare la nostra stella è L1, dal momento che un satellite in questa posizione potrebbe stazionare stabilmente tra la Terra e il Sole. È questo il caso del telescopio spaziale Soho (ESA/NASA) – che si trova fisso rispetto al sistema Sole-Terra ma che ovviamente si sposta nello spazio con esso – che rappresenta il nostro osservatorio sul Sole.
La posizione migliore per tenere sotto controllo il nostro pianeta dallo spazio è invece L2, dal momento che non ci si ritrova mai di mezzo il Sole a interferire con le trasmissioni, dove per l'appunto si trovano il satellite Gaia (ESA) e il telescopio spaziale Web (NASA), che ruotano attorno al punto di equilibrio in un piano perpendicolare a quello del sistema Sole-Terra.
Ricordando che L1 e L2 – e L3, dove non ci sono sonde terrestri dal momento che, sempre col Sole di mezzo, non potrebbero inviare informazioni alla Terra – sono punti di equilibrio instabile, tutti i satelliti che lì si trovano devono spendere energia per mantenersi stabili, perché qualsiasi piccola perturbazione potrebbe farli schizzare via. Questo significa che devono avere una risorsa di propellente che serve per aggiustare la posizione nel momento in cui viene deviata dal punto di equilibrio. E dato che la scorta di propellente non è infinita, prima o poi queste missioni sono destinate a finire.

Il problema dei tre corpi ridotto del sistema Sole-Giove.

I punti L4 e L5, come dicevamo, sono invece di equilibrio stabile, quindi un oggetto posizionato lì può restarci per sempre. In questi punti tendono quindi ad addensarsi oggetti naturali, come asteroidi e polvere interplanetaria.
Se invece della Terra consideriamo il sistema Sole-Giove – tenendo conto che le masse degli altri pianeti di mezzo (Mercurio, Venere, Terra, Marte) sono rispetto a essi molto più piccole – lo studio del problema dei tre corpi ristretto permette di dare una spiegazione dell'ammasso di asteroidi detti Troiani – perché hanno nomi per lo più presi dalle opere di Omero – intorno ai punti L4 e L5.
Il problema dei tre corpi continua a sfidare e affascinare gli scienziati di tutto il mondo. Le sue applicazioni pratiche sono molteplici e ci permettono di guidare il progresso tecnologico e la nostra comprensione dell'Universo.

[1] In matematica, una serie numerica è una addizione con un numero infinito di termini che abbiano una determinata caratteristica in comune – si parla ad esempio della serie numerica dei numeri naturali, dei numeri pari, delle frazioni con denominatore intero, e così via. Ma come si calcola la somma di un numero infinito di termini? E anche riuscendoci, il risultato sarà a sua volta un numero infinito? Per capire il carattere di una serie, cioè se è convergente (la serie è regolare e ammette un risultato che è un numero finito calcolabile), divergente (la serie è regolare e ammette come risultato infinito ) o indeterminata (la serie è irregolare, cioè non ammette risultato), è necessario considerare la successione delle somme parziali. Per somma parziale si intende la somma dei primi n termini della serie. Studiando il comportamento di questa somma parziale all'infinito (facendone cioè il limite), si può non solo capire il carattere della serie, ma anche trovare il risultato della somma infinita di termini (nel caso in cui la serie sia regolare), che sarà proprio uguale al limite all'infinito della successione delle somme parziali.

S =		an =		sn
	Σ		lim
	n=1		n

sn = a1 + a2 + a3 + ... + an

[2] Un punto di equilibrio instabile è un punto di equilibrio "precario", basta una piccola variazione e il corpo che si trova in questo punto comincia a rotolare via. Si pensi, ad esempio, a una pallina ferma sulla cima di una montagna: appena viene sfiorata scivolerà a valle lungo uno qualsiasi dei pendii. Un punto di equilibrio stabile è invece, ad esempio, un avvallamento: se ci si trova dentro una pallina, una piccola variazione che la sposti senza farle superare il bordo della buca, la farà solo oscillare avanti e indietro per un po' fino a quando non tornerà nel punto di equilibrio.

Stefania Bergo SCHEDA AUTRICE

Leggi >

Si può superare la velocità della luce?

Scienza Di Stefania Bergo. La velocità della luce è una grandezza fondamentale per spiegare il nostro universo. È un limite invalicabile su cui si basa la teoria della relatività di Einstein, è la costante che regge l'equivalenza tra massa ed energia. Ma perché non si può raggiungere o superare?

Fino al XVII secolo si pensava che la luce viaggiasse a una velocità infinita, cioè che si spostasse istantaneamente da un posto all’altro senza alcun ritardo. Fu Galileo Galilei – manco a dirlo – a intuire per primo che la velocità della luce non fosse infinita, ma avesse un valore finito, anche se non riuscì a provarlo, principalmente per la limitatezza degli strumenti a disposizione all'epoca.

Leggi anche Marte chiama Terra risponde. Pillole di astronomia, il nuovo libro di Amy Cafe Gerini

L'esperimento di Galileo Galilei fu puramente empirico e non portò alcun risultato apprezzabile sulla misura della velocità della luce.

Egli aveva posto due persone a distanza di un chilometro l’una dall’altra, entrambe con una lanterna e uno straccio per coprirne la luce. La prima persona doveva scoprire la lanterna e la seconda doveva fare altrettanto dopo aver visto la luce della prima: in questo modo sarebbe stato possibile calcolare la velocità della luce semplicemente misurando il ritardo tra il momento in cui la prima lanterna era stata scoperta e quello in cui aveva visto la luce della seconda lanterna. Ma la luce è talmente veloce – oggi lo sappiamo, viaggia a una velocità di quasi 300.000 chilometri al secondo – che per distanze piccole, come possono esserlo pochi chilometri sulla Terra, non poteva essere percepibile a occhio nubo un ritardo nella rilevazione dei due segnali luminosi – senza contare che il ritardo avrebbe potuto essere introdotto semplicemente dai tempi di reazione fisiologici della seconda persona.

Galileo non riuscì a misurare la velocità della luce, ma fece una scoperta che servì qualche decennio più tardi a Ole Rømer e Giovanni Cassini per misurarla con apprezzabile precisione.

Nel 1610 Galileo scoprì quattro dei 79 satelliti di Giove – Io, Europa, Ganimede e Callisto. Qualche decennio più tardi, intorno al 1676, Ole Rømer, all’Osservatorio di Parigi fondato da Giovanni Cassini, utilizzando la posizione e il movimento dei quattro satelliti di Giove cercò di misurare la velocità della luce a partire dalla rilevazione del tempo, utilizzando, per così dire, una sorta di "orologio" spaziale e la relazione che lega queste grandezze: velocità = spazio/tempo. Egli si basò sull'osservazione delle eclissi lunari di Io, rilevando delle differenze nella misurazione dei tempi delle eclissi a seconda della distanza di Giove dalla Terra. Tenendo presente che osservare, e quindi misurare, un fenomeno significa che lo "sguardo", cioè la luce che lo illumina per renderlo "visibile", ritorna all'osservatore, e che l'osservatore in quel caso era Rømer sulla Terra, mentre l'eclissi osservata era su Io, dividendo il doppio dello spazio che separa il nostro pianeta da Giove – l'andata e ritorno dello "sguardo" – per il tempo impiegato per la rilevazione della misura, ottenne una buona approssimazione della velocità della luce.

Oggi sappiamo che la velocità si propaga nel vuoto a quasi trecentomila chilometri al secondo. E nulla può viaggiare alla velocità della luce, ad eccezione dei fotoni: è un limite imposto dalla teoria della relatività ristretta di Einstein.

La velocità della luce nel vuoto è una costante fisica, indicata con c, nel senso che il suo valore è uguale in qualsiasi sistema di riferimento inerziale e per qualsiasi osservatore, sia esso in quiete, in movimento con velocità costante o in accelerazione, misurerà sempre lo stesso valore.
Ci addentriamo ora in un ambito un po' più complicato, quello prettamente fisico, dal momento che ci baseremo sulle leggi della meccanica quantistica.

Ci risiamo, signora Maria, torniamo a parlare di meccanica quantistica, quella di cui le ho parlato in un paio di vecchi articoli: si ricorda del paradosso del gatto di Schrödinger e dell'entanglement? Se vuole può andarseli a rileggere. In ogni caso, anche questa volta cercherò di raccontarle in modo molto semplice, per quanto sia possibile semplificare la meccanica quantistica, perché non si può superare la velocità della luce.

La velocità della luce rappresenta un limite fisico e matematico invalicabile.

Partiamo considerando una massa visibile che si nuove a una velocità ordinaria: ad esempio una macchina che sfreccia a 120 km/h. Ovviamente, per muoverla è stata spesa una certa quantità di energia, quella necessaria al motore per muovere i pistoni e accelerarla, ad esempio. Ma in generale, ogni volta che un corpo è in movimento significa che una qualche forza lo ha spinto e che quindi è stata spesa dell'energia per variare il suo stato di quiete. Questa energia, supponendo che non ci siano "sprechi" – cioè attriti – viene totalmente convertita in energia cinetica, che è appunto l'energia di un oggetto in movimento, ed è legata alla sua velocità dall'equazione:

E

=

1 2

m·v

2

dove E è l'energia cinetica, m la massa dell'oggetto in movimento e v la sua velocità.

Si può quindi accelerare indefinitamente una massa fino a portarla alla velocità della luce o addirittura maggiore?

Data la natura dell'equazione qui sopra, si potrebbe pensare che con energie sempre più grandi si possa accelerare una massa fino a velocità sempre maggiori, quindi apparentemente non ci sarebbe limite alla velocità raggiungibile, se non quello dato dalle tecnologie a nostra disposizione oggi. In realtà non è così, perché l'equazione così formulata vale solo per velocità molto più piccole di quella della luce.
Per velocità prossime a quella della luce, infatti, vale l'equazione:

E

=

mo c2 √1-v2/c2

— mo c2

che rappresenta l'energia cinetica relativistica, dove m_o è la massa a riposo dell'oggetto. La celeberrima equazione di Einstein E = mc², infatti, suggerisce che, dato che c è una costante, all'aumentare dell'energia di un corpo – o particella elementare – aumenta anche la sua massa, e per velocità prossime a quella della luce questo implica che una parte sempre maggiore di energia vada ad aumentare la massa mentre la restante frazione contribuisca effettivamente ad accelerarla.

La velocità relativistica è stata verificata sperimentalmente e afferma che qualsiasi sia la massa iniziale di un corpo, per accelerarlo alla velocità della luce servirebbe un'energia infinita.

Dal punto di vista matematico, è evidente che nella formula precedente è presente un punto di discontinuità di seconda specie proprio per v = c. Questo significa che per v = c il corrispondente valore di energia cinetica è infinito, cioè servirebbe una energia infinita per accelerare una massa fino a farle raggiungere la velocità della luce e più che infinita se si volesse fargliela addirittura superare. Il che, ovviamente, non è possibile, quindi non è mai possibile accelerare una massa fino a farle raggiungere la velocità della luce.

Lo so, signora Maria, dalla formula in poi si è persa... Anzi, forse proprio sulla formula. Ho dato per scontato un po' troppe cose. Ad esempio non ho spiegato cosa sia un punto di discontinuità, la cui presenza nella formula di Einstein è tutt'altro che evidente per chi non mastica matematica dai tempi della scuola. Si concentri per un attimo sul denominatore della formula, 1-v²/c ²: per v = c vale 0. Si ricorda che alle elementari ha imparato che non si può dividere alcun numero per 0? Ecco, non è che proprio "non si può", semplicemente dividendo un numero per 0 si ottiene infinito, ∞.

Tuttavia, ci sono "particelle" che viaggiano proprio alla velocità della luce: i fotoni.

Ma quindi, contrariamente a quanto detto finora, si può raggiungere la velocità della luce?! In un certo senso sì. Ma non contrariamente a quanto detto finora. I fotoni, infatti, sono "particelle" senza massa, per cui non ha più senso applicare la formula della velocità relativistica di Einstein: possono quindi viaggiare alla velocità della luce, anzi, viaggiano solo alla velocità della luce, né più, né meno.

«Come possono delle particelle non avere una massa?»
Le rispondo semplificando molto, signora Maria. In effetti i fotoni non sono propriamente delle "particelle" nel senso classico del termine, sono più "pacchettini di energia luminosa" e tutti insieme formano la luce stessa. Quindi, ovviamente, viaggiano alla velocità della luce perché sono la luce!
«La luce è formata da pacchettini!?» Gliel'ho detto, signora Maria, ho semplificato molto. Magari lo vedremo la prossima volta, in un articolo a parte, quando le spiegherò la Relatività di Einstein... Non si allarmi e cerchi di seguirmi, ho quasi finito.

Nel 1967 il fisico Gerald Feinberg ipotizzò l'esistenza di particelle che viaggiano a velocità superiori a quella della luce: i tachioni.

Secondo la sua teoria, i tachioni viaggerebbero sempre a velocità superiori a quella della luce senza poter mai decelerare, come se la velocità della luce fosse comunque un limite invalicabile: alcune particelle nascono al di qua – non possono mai accelerare fino a raggiungere la velocità della luce – altre al di là – non possono mai essere frenate fino a raggiungere la velocità della luce.
Ma i tachioni, esistono davvero? Anche Einstein aveva ipotizzato l'esistenza delle onde gravitazionali ma non aveva potuto provarlo per la limitatezza della strumentazione a disposizione. Si può quindi pensare che in futuro si possa dimostrare anche l'esistenza dei tachioni?
Forse. Lo vedremo nei prossimi articoli.

Leggi anche Stefania Bergo | Dalla relatività di Einstein alle onde gravitazionali

La velocità della luce è un limite matematico e fisico. Non solo, rappresenta anche un limite alla causalità, una proprietà fondamentale dell'universo.

Pensiamo ad esempio a un messaggio – una informazione, una domanda – inviato tra due osservatori, l'uno fermo rispetto a un sistema di riferimento inerziale e l'altro in movimento a una velocità maggiore di quella della luce, oppure tra un osservatore fermo e uno in movimento a una qualsiasi velocità minore di c ipotizzando di inviare un messaggio istantaneo, cioè a velocità addirittura infinita. Saremmo di fronte a un paradosso: la risposta al messaggio inviata a sua volta dal secondo osservatore raggiungerebbe il primo osservatore indietro nel tempo, nel suo passato, cioè prima che la domanda stessa fosse fatta – in accordo con la teoria della relatività che vedremo in uno dei prossimi articoli. Verrebbe violato il principio di causalità, che poi è lo stesso problema sollevato dal fenomeno quantistico dell'entanglement.

Leggi anche Stefania Bergo | Entanglement quantistico: la fantasmatica azione a distanza

Ok, la velocità della luce non si può raggiungere, tanto meno superare. E se utilizzassimo un sistema di due "veicoli" che viaggiano uno sull'altro a velocità uguali alla metà della velocità della luce?

L'espediente è una furbata, vero signora Maria? Pensiamo ad esempio di viaggiare in treno: se, senza dare troppo nell'occhio, lanciassimo una pallina da tennis nella direzione del moto del treno, per un osservatore a terra, tipo suo marito Franco, la sua velocità v_p si sommerebbe a quella del treno v_t arrivando a una velocità totale v = v_p + v_t.
E se queste due velocità valessero proprio la metà di quella della luce? Potremmo sommarle e arrivare alla velocità della luce?

No. Mi dispiace, ma no. Perché per velocità grandi, come lo è la metà di quella della luce, valgono regole differenti, ancora una volta rifacenti alla relatività di Einstein. Le due velocità relative – tra i mezzi – non vanno semplicemente sommate per dare il valore della velocità misurata da un osservatore fermo – velocità assoluta – ma la formula che descrive il fenomeno fisico è la seguente:

v

=

vp+ vt 1 + vpvt/c2

che quindi risulta sempre minore della velocità della luce.
Quindi no, la velocità della luce non può mai essere raggiunta, tanto meno superata, accelerando una massa qualsiasi con energia finita. Le uniche "particelle" che viaggiano alla velcità della luce sono i fotoni, che però non hanno massa e sono la luce stessa. E poi ci sarebbero i tachioni per cui la velocità della luce rappresenta comunque un limite, anche se inferiore. Ma approfondiremo la prossima volta...

Stefania Bergo SCHEDA AUTRICE

Leggi >

Osservare il cielo e vedere il passato

Scienza Di Valentina Gerini. Osservare il cielo significa vedere il passato, la luce emessa dalle stelle anni fa.

Circa seimila sono le stelle visibili a occhio nudo dalla Terra. Seimila stelle che possiamo osservare ogni notte, se abbiamo la fortuna di trovarci in una zona con scarsa illuminazione artificiale. La maggior parte di queste si trova a una distanza di mille anni luce dal Sole, la nostra stella.
Ma cosa stiamo davvero vedendo quando osserviamo queste stelle?
Il concetto è complicato e affascinante allo stesso tempo. L'ho appreso leggendo articoli di divulgazione scientifica a mia figlia Amy (sette anni), che è una grande appassionata di astronomia e ha scritto e illustrato un libro per bambini: In fila per otto col resto di uno. Il Sistema Solare.
Non sono una scienziata e le mie conoscenze in materia sono limitate, ma proverò a spiegarvi ciò che ho imparato.

Guardare una stella significa vedere la luce che questa stella ha emesso nel passato, luce che ha viaggiato fino a noi per giungere nel nostro presente.

Supponiamo che oggi, 28 giugno 2021, io stia osservando la stella Alfa Centauri alle 11:00 di sera. Alfa Centauri si trova a una distanza di 4,4 anni luce dalla Terra, pertanto io sto osservando la luce che Alfa Centauri ha emesso 4,4 anni fa, sto quindi osservando come Alfa Centauri brillava 4,4 anni fa, non come brilla oggi, alle 11:00 di sera del 28 giugno 2021. La luce, infatti, viaggia a una velocità di circa 300.000 km/s – per la precisione 299 792 458 m/s – perciò la luce emanata da Alfa Centauri ci raggiunge dopo il tempo impiegato per viaggiare fino a noi. Più una stella è lontana da noi, più indietro nel tempo – e quindi nel passato – è stata emessa la luce che oggi vediamo. Questo significa che noi non vediamo il cielo attuale, ma quello di tanti anni fa, in base alla distanza delle stelle dalla nostra Terra.

Un esempio molto noto è rappresentato dalla supernova esplosa il 4 luglio 1054 nella costellazione del Granchio. Questa impressionò molto gli astronomi cinesi: rimase splendente per ben 23 giorni anche con la luce del giorno. Poi la sua luminosità si è affievolita fino ad assumere la caratteristica forma di nube con articolazioni che tanto la fanno assomigliare ad un granchio (Crab Nebula). […] La nebulosa del Granchio si trova a circa 60 milioni di miliardi di Km dalla terra (6 seguito da 16 zeri) - 6000 anni luce, distanza che implica che qualsiasi evento osservato in quella zona sia accaduto almeno 6000 anni prima. Ovviamente, anche se con una differenza di 6000 anni, noi osserviamo gli eventi nella sequenza giusta e dunque l'oggetto che osserviamo adesso corrisponde allo stadio della supernova dopo un'evoluzione di quasi un millennio dalla sua esplosione.
scienzapertutti.infn.it

Nell'universo ci sono stelle che si spengono, ma noi le vediamo ancora accese.

L'uomo è da sempre affascinato dalla capacità di vedere nel futuro, eppure ha da sempre la possibilità di vedere nel passato: basta osservare il cielo. Grazie ai potenti telescopi sulla Terra e a quelli che vengono lanciati nello spazio profondo per studiare l'Universo – come il telescopio Hubble, che dal 1990 ci ha regalato immagini meravigliose e ha cambiato la nostra percezione del cosmo – riusciamo a vedere fino a 13 miliardi di anni indietro nel tempo, età stimata dell'Universo. Con i telescopi spaziali, infatti, è possibile osservare un cielo più nitido e definito, grazie all'assenza di atmosfera. Nello spazio niente si interpone tra l'osservatore (il telescopio) e il corpo osservato (una stella, per esempio). Sulla Terra, invece, l'occhio umano è disturbato dall'atmosfera che "opacizza" l'immagine della stella che percepiamo. In ogni caso, nitidezza a parte, possiamo osservare il cielo che fu e questa espressione regala un tocco di magia alla all'osservazione del cielo.

L'Universo è in continua espansione, le stelle si muovono, si allontanano, così il cielo cambia nel tempo.

A onor della verità, dire che guardare il cielo equivale esclusivamente a osservare il passato non è del tutto vero. Questo perché, come sappiamo, l'Universo è in continua espansione e le stelle non sono dei diamanti incastonati stabilmente in un manto scuro e freddo. Le stelle, come tutti i corpi celesti, si muovono, si allontanano, pertanto se riprendiamo l'esempio sopracitato di Alfa Cenaturi oggi possiamo osservare la luce che questa stella ha emesso 4,4 anni fa senza tener conto di un suo eventuale spostamento.
Però noi scrittori, romantici e sognatori quali siamo, preferiamo attaccarci saldamente alla convinzione che guardare il cielo significhi guardare il passato. Da oggi, dopo aver letto questo articolo, sarà bello guardare una stella e pensare che quel che vediamo non è l'ora, il subito, bensì è il prima, lo ieri.

Ne parlo in diretta con PubMe e alcuni ospiti.

Se questo argomento vi affascina, se il cosmo e i corpi celesti rapiscono da sempre la vostra attenzione, allora vi consiglio di seguire la PubMe Live di questa sera, 28 giugno, alle 21:00, sui canali Facebook, YouTube e Twitch di PubMe. Saranno ospiti lo scienziato astronomo Luca Nardi e l'astrofotografo Filippo Valacchi per parlare di astronomia. Se non doveste riuscire a vedere la diretta, potrete "vedere nel passato", proprio come accade quando si osservano le stelle, grazie alla registrazione: Live PubMe su YouTube.

Valentina Gerini SCHEDA AUTRICE

Leggi >

Covid-19: quali sono le reali fonti di contagio?

Scienza Di Stefania Bergo. Covid-19: quali sono le reali fonti di contagio? Possiamo evitare di ammalarci? Mascherina e distanza sociali sono davvero necessarie? Sono sufficienti?

Ho letto un post interessante, qualche giorno fa, su Internazionale, a sua volta la traduzione di un articolo dell'immunologo Erin Bromage. Trattava degli effettivi rischi di contagio da coronavirus Sars-Cov-2 che corriamo ora che il lockdown è quasi del tutto terminato e possiamo uscire di casa.
Le misure restrittive si sono ormai allentate e dalla prossima settimana potrebbero farlo ulteriormente consentendo gli spostamenti tra regioni. Queste nuove libertà si basano sulla previsione della curva epidemiologica che ormai è in fase discendente. Tuttavia tale previsione non tiene conto delle nuove occasioni di diffusione del virus dovute al ripristino di quasi tutte le nostre attività. È abbastanza intuitivo: chi finora è rimasto in casa, protetto da eventuali fonti di contagio, ora può uscire ed entrare in contatto col vicino e, tra poco, con gli abitanti di altre regioni, quindi con molte fonti di probabile contagio. Quindi sarà fisiologico vedere un nuovo aumento della curva epidemiologica, sebbene la virulenza del Sars-Cov-2 pare essersi attenuata.

Ma quali sono le reali fonti di contagio? Quali sono i comportamenti a rischio?

Ormai è stato confermato che la maggior parte dei contagi si verifica in famiglia, dove chi è stato contagiato può portare inconsapevolmente il virus a casa e avere tutto il tempo di trasmetterlo, dati i contatti prolungati. Per contrarre il Covid-19, infatti, è necessario essere esposti a una dose infettiva di virus. E, in base a studi statistici non sperimentali sugli altri coronavirus, sappiamo che per trasmettere la malattia sarebbero sufficienti mille particelle infettive di Sars-cov-2 inalate o entrate in contatto con i nostri occhi. A questo punto interviene anche il fattore tempo, dal momento che la dose infettiva che entra nel nostro corpo non necessariamente lo deve fare in un'unica tranche ma si può arrivare alla dose minima per il contagio anche inalando le particelle virali a rate, poco per volta, per un periodo continuativo di tempo abbastanza lungo.
Tra gli ambienti più a rischio ci sono sicuramente tutti quei locali che presentano molte superfici toccate continuamente da tutti, come le maniglie o i rubinetti nei bagni pubblici, i tornelli della metropolitana, i corrimano delle scale dei luoghi pubblici, i tasti degli ascensori, e così via.
Sarebbe sempre bene, quindi, lavarsi accuratamente le mani o utilizzare gel disinfettanti prima di toccarsi naso e bocca, in modo da uccidere eventuali virus accumulati sulla pelle.

Ma come ci finiscono i virus dal paziente infetto sulle superfici? Ci si può contagiare semplicemente respirando aria contaminata? 

Il contagio avviene attraverso le famose droplet, le goccioline di saliva che sputiamo mentre respiriamo, parliamo o quando tossiamo e starnutiamo, perché in esse si trovano i virus che infettano il nostro apparato respiratorio. In particolare, un colpo di tosse può disperdere nell'ambiente circa tremila goccioline, che possono viaggiare a ottanta chilometri orari. Avendo dimensioni relativamente grandi, per gravità queste goccioline tendono a cadere sulle superfici senza percorrere grandi distanze, quindi contaminano solo l'area a stretto raggio intorno alla persona malata. Nel caso degli starnuti, invece, le goccioline emesse possono arrivare fino a 300 chilometri orari, fino a duecento milioni di particelle tutte insieme e coprire distanze ben superiori al metro, essendo più piccole e risentendo meno della gravità. In questo caso, quindi, l'area infettata da un singolo starnuto è maggiore.
Il semplice respirare, invece, secondo studi condotti sulle sindromi influenzali stagionali, rilascia in ambiente tra le cinquanta e le cinquemila goccioline che risultano essere anche molto lente, quindi decadono quasi subito nell'area intorno alla persona infetta. Inoltre, l'espirato non proviene dall'apparato respiratorio inferiore – i polmoni – ma solo dalle vie aeree superiori, quindi nelle goccioline di saliva ci sarà un numero notevolmente più basso di virus. Sempre riferendosi a questi studi si può affermare che in un minuto, semplicemente respirando, emettiamo in ambiente circa 30 particelle virali.

Come facciamo a sapere se abbiamo contratto il coronavirus e siamo quindi potenzialmente infetti?

In effetti, a meno che non ci facciamo il famoso tampone, non possiamo saperlo, se non quando si presentano i sintomi evidenti della malattia, a maggior ragione nei casi più gravi, in cui si necessita di cure domiciliari o addirittura ospedaliere. C'è però una larga fetta di malati asintomatici o con sintomi lievi, come tosse e raffreddore, che possono essere facilmente confusi con altre sindromi influenzali. Va da sé che, nel dubbio, chi ha tosse o starnutisce frequentemente farebbe bene a stare a casa o quanto meno evitare gli ambienti chiusi in cui ci sia promiscuità.
E le persone asintomatiche? Statisticamente, almeno il 44 per cento dei casi di contagio nelle comunità è provocato da persone che non presentano sintomi o che ancora non li hanno sviluppati – nel periodo di incubazione, ad esempio. Si calcola che un individuo positivo al coronavirus possa disperdere il virus in ambiente per almeno cinque giorni prima di manifestare i sintomi della malattia e di essere quindi cosciente di poter infettare qualcuno. Un dato che fa riflettere è che la carica virale aumenta progressivamente fino alla comparsa dei primi sintomi ed è massima proprio subito prima che si manifestino, cioè quando siamo ancora all'oscuro di essere ammalati.

Per contaminarsi non si deve tenere in considerazione solo la quantità di virus inalati ma anche il tempo in cui siamo esposti al virus.

Come dicevo, se da un lato servono grandi quantità di virus in poco tempo per infettarci, dall'altro si può facilmente intuire che la stessa quantità può essere raggiunta anche inalando un minor numero di particelle virali istantanee ma per un tempo più prolungato.
Le particelle di saliva infetta restano nell'aria solo qualche minuto, se emesse semplicemente con la respirazione, ma possono restarvi più a lungo nel caso siano state emesse starnutendo, oltre ad essere presenti in misura notevolmente maggiore. Se si entra in una stanza in cui una persona infetta ha appena starnutito, ad esempio, possono bastare pochi minuti per respirare una quantità sufficiente di virus per contaminarsi. Mentre per contaminarsi semplicemente con l'espirato di una persona ammalata ne servono almeno cinquanta.
Parlare, poi, aumenta il numero di agenti patogeni emessi in aria di circa dieci volte rispetto alla semplice respirazione. In questo caso, la quantità di goccioline virali rilasciate arriva fino a circa duecento al minuto quindi possono bastare anche cinque minuti per respirare una quantità di agenti patogeni sufficiente per contaminarci.

Ecco perché i rischi maggiori si corrono negli ambienti chiusi in cui si sta a lungo o in cui si interagisce e in cui gli impianti di climatizzazione non sono adeguati.

Come i reparti ospedalieri, le scuole, gli uffici, le fabbriche, i call center, gli impianti di macellazione, i pub, i ristoranti, i parrucchieri, le palestre, le chiese, i mezzi pubblici, solo per fare qualche esempio. Ambienti in cui le persona necessariamente devono avvicinarsi per comunicare o in cui gli impianti di climatizzazione non funzionano correttamente o non sono adeguati. Anzi, spesso gli impianti di climatizzazione sono i principali imputati della diffusione del virus, non solo perché possono accumulare agenti patogeni se non frequentemente e accuratamente sanificati, ma anche perché movimentano l'aria interna spostandola da una persona all'altra, trasportando quindi l'espirato. In questi ambienti, quindi, se si permane a lungo, anche la distanza di un metro pare non essere sufficiente a garantirci di non entrare in contatto con possibili virus dispersi in aria.
Riassumendo: la permanenza prolungata in spazi chiusi e affollati, in cui ci sia un ricambio d'aria insufficiente o addirittura solo un ricircolo – gli impianti non pescano di continuo aria esterna ma rimettono in circolazione quella interna, movimentandola semplicemente senza cambiarla – presenta un rischio elevato di trasmissione del virus. In questi casi, è necessario indossare la mascherina di tipo chirurgico che trattiene le goccioline di saliva infette all'interno – la saliva, non l'anidride carbonica! – e abbatte del 90% circa la loro presenza nell'aria.

All'aperto corriamo meno rischi: gli spazzi maggiori ostacolano la trasmissione del virus. Ma è importante mantenere la distanza sociale e indossare la mascherina quando ci si ferma a parlare con gli altri.

L'interazione con gli altri dovrebbe avvenire a distanza di sicurezza. Non dimentichiamo che per il contagio sono sempre indispensabili quantità di carica virale e tempo di esposizione. Il semplice incrocio tra corridori non è sufficiente per la trasmissione di eventuali virus, ma parlare per più di cinque minuti a distanza ravvicinata con qualcuno di infetto che non indossi la mascherina potrebbe essere sufficiente a inalare la quantità di virus necessaria per ammalarci. Oppure potrebbe bastare il contatto tra le sue goccioline di saliva e le nostre mani – sappiamo quanto noi italiani gesticoliamo parlando, quindi le mani sono perennemente nello spazio tra noi e l'interlocutore – con cui poi, dimenticandoci di disinfettarle, ci potremmo toccare gli occhi.

In definitiva, nel dubbio di essere infetti, indossiamo sempre la mascherina negli ambienti chiusi e affollati e quando ci fermiamo a parlare all'aperto con altre persone, laviamoci o disinfettiamoci spesso le mani, manteniamo le distanze di sicurezza. 

Proteggiamo gli altri e di conseguenza anche noi stessi, i nostri cari, perché anche gli altri faranno lo stesso. Non ribelliamoci a queste semplici, banali regole, diamo prova di civiltà. Ricordate l'insofferenza alle cinture di sicurezza, all'inizio? Abbiamo imparato a suon di multe che spesso sono proprio quelle a salvarci la vita. A maggior ragione ora, che si tratta di regole momentanee, non sarà per sempre. Le guerre da combattere sono altre. Dimostriamoci insofferenti alla crisi economica, se vogliano, alle ingiustizie del mondo – e ce ne sono, oh se ce ne sono – non a un pezzo di stoffa con gli elastici. Diamo il buon esempio ai nostri figli. Altrimenti il virus non se ne andrà mai. E non mi riferisco al Sars-Cov-2...

Stefania Bergo Non ho mai avuto i piedi per terra e non sono mai stata cauta. Sono istintiva, impulsiva, passionale, testarda, sensibile. Scrivo libri, insegno, progetto ospedali e creo siti web. Mia figlia è tutto il mio mondo. Adoro viaggiare, ne ho bisogno. Potrei definirmi una zingara felice. Il mio secondo amore è l'Africa, quella che ho avuto la fortuna di conoscere e di cui racconto nel mio libro. Con la mia valigia gialla, StreetLib collana Gli scrittori della porta accanto (seconda edizione). Mwende. Ricordi di due anni in Africa, Gli scrittori della porta accanto Edizioni. La stanza numero cinque, PubMe – Collana Gli scrittori della porta accanto. SCHEDA DELL'AUTRICE

Leggi >

CRISPR-Cas9, l'editing genetico: quali limiti all'alterazione del genoma umano?

Scienza Di Nicolò Maniscalco. CRISPR-Cas9: l’editing gen... etico. L’aver mappato il genoma umano è stato un grosso passo avanti per la scienza, per la possibilità di combattere molte malattie. Ma ci sono dei limiti all'alterazione genetica dell'essere umano.

È una lunga strada quella percorsa dalla scienza nella manipolazione genetica, partendo dalla clonazione della pecora Dolly del 1996 fino ad oggi. Gli ultimi baluardi della genetica riguardano la CRISPR-Cas9 battezzata con il nome di editing genetico.
L'enzima Cas9 è considerato dai genetisti, una forbice molecolare ed è utilizzato nei laboratori di genetica per ingegnerizzare il genoma. Cas9 si è dimostrato particolarmente indicato per modificare l’espressione di specifici geni, nell’ambito della tecnica dal nome reboante di Clustered Regularly Interspaced Short Palindromic Repeats, letteralmente: brevi ripetizioni palindrome raggruppate e separate a intervalli regolari, tecnica che, per fortuna dei non addetti ai lavori, è sintetizzata nell’acronimo CRISPR.
La scoperta di questa biotecnologia che sfrutta un meccanismo batterico di difesa immunitaria per contrastare gli attacchi dei batteriofagi, risale al 2005. La pressione evolutiva ha insegnato a questi batteri il taglio di parti di DNA virale poi “cucite” nel proprio genoma e trascritte in RNA per essere riconosciute dall’enzima Cas9 nell’identificare il DNA dell’aggressore e difendersi così da nuove infezioni. Il processo, nella sua essenza, è alla base della transgenesi nella produzione di OGM (organismi geneticamente modificati) ma la tecnica è stata rivoluzionata con l’avvento della CRISPR-Cas9.

È recente la notizia che il biologo He Jiankui della South University of Science and Technology of China di Shenzhen ha modificato il genoma dell’embrione di due gemelle proprio con la tecnica CRISPR-Cas9. 

Lo scopo dell’operazione è legato alla battaglia contro le malattie, infatti, il gene eliminato nel DNA delle due neonate, rende immune le stesse dall’infezione da HIV non permettendo la produzione della proteina recettrice Ccr5 porta d’ingresso del virus e, non solo, essendo la modifica fatta sul genoma, è trasmissibile quindi ereditabile dalla prole.
Il mondo scientifico si è mostrato scettico per la prematurità dell’evento, i più hanno ritenuto che il vero obiettivo fosse l’editing genetico e non l’evitare la malattia e lo stesso Ateneo cinese ha preso le distanze dall’esperimento e dal dottor He Jiankui.
Un’operazione di modifica genomica tramite la tecnica CRISPR-Cas9 era già stata realizzata da vari scienziati statunitensi dell’Institute del Massachusetts Institute of Technology e della Harvard University, modificando il gene di regolazione del colesterolo, chiamato Pcsk9, in alcuni topi di laboratorio, abbassandone il livello, agendo sul fegato. Ma quello di He Jiankui è stato il primo vero esperimento su esseri umani.

La conclusione del vertice sull’editing genetico del 2015 è stata la raccomandazione che l'alterazione genetica nell’uomo rimanga confinata alle ricerche di laboratorio, che devono proseguire in vista degli importanti progressi per la salute. 

Ed è perciò con grande curiosità che gli scienziati hanno atteso la relazione di He Jiankui nel Summit sullo Human Genome Editing di Hong Kong che si è svolto dal 27 al 29 novembre. Per la verità lo scienziato cinese non ha rivelato molto più di quello che era già trapelato, aggiungendo che a breve ci sarà la pubblicazione su una rivista scientifica sulle conclusioni del suo lavoro.
Personalmente sono certo che l’aver mappato il genoma umano negli anni scorsi sia stato un grosso passo avanti per la scienza e per la possibilità di combattere molte malattie ma mi auguro come biologo ma soprattutto come essere umano che la comunità scientifica sappia gestire nel rispetto e nella ricchezza delle diversità, le inevitabili manipolazioni prospettate dall’editing genetico.
La vita reale non è un romanzo di fantascienza e le storture di chi ama le razze elette devono restare in un passato neanche troppo lontano.

Nicolò Maniscalco L'infinita quantità dei suoi hobbies li rende assolutamente non tutti elencabili, tra questi: l'Agility Dog, che pratica con i suoi amati Border Collie, e la lettura di libri e fumetti. Dopo anni d’indecisione, inizia a scrivere un po' per gioco un po’ per mettersi alla prova. Il Labirinto della Memoria, Zerounoundici Edizioni. Nucleo operativo A5, Selfpublished. Il confronto, Zerounoundici Edizioni. SCHEDA DELL'AUTORE

Leggi >

Stephen Hawking, breve storia di un fiume infinito

Scienza Di Vincenzo Mirra. Stephen Hawking: «Per quanto difficile possa essere la vita, c'è sempre qualcosa che è possibile fare. Guardate le stelle invece dei vostri piedi».

A parte la sfortuna di contrarre la mia grave malattia dei motoneuroni, sono stato fortunato sotto quasi ogni altro aspetto.
Stephen Hawking 

È questo forse il più grande e stupefacente insegnamento che lascia Stephen Hawking, una delle menti più geniali che ha attraversato, contro ogni aspettativa di vita, il portale dello spazio-tempo tra il secolo breve e la nuova era delle comunicazioni digitali e gravitazionali, proprio come se, attraverso un cunicolo spazio-temporale, avesse viaggiato tra universi paralleli nell'età a cavallo tra il vecchio millennio ed il futuro.

Leggi anche Vincenzo Mirra | Si accendono le luci: l’Universo

Stephen Hawking è nato a Oxford l’8 gennaio 1942, nello stesso giorno in cui 300 anni prima moriva Galileo Galilei, come se l'Universo gli avesse consegnato nella vita l’eredità del padre del pensiero scientifico e della scienza moderna.

Il Professor Hawking ci lascia in eredità la sua straordinaria forza vitale, l'inesauribile e ostinata forza per la vita che era nel suo cuore e che ha donato a tutta l'umanità, con il suo gigantesco esempio di determinazione.
Quando nel 1963, a 21 anni, gli diagnosticarono una inesorabile e progressiva malattia degenerativa (prima SLA e poi motoneurone), i medici stimarono che non avrebbe vissuto più di due anni. Una prospettiva assi limitante per un giovane e promettente graduato di prima classe di Oxford, appassionato di matematica e con un pensiero talmente raffinato da poter prendere su di sé l’eredità di tre secoli di scoperte scientifiche e di teorie fisiche per lanciarsi nell’affascinante idea di elaborare un’avvincente Teoria cosmologica del Tutto.

Così il giovane studente di Cambridge, Stephen per gli amici, a dispetto delle stime sulla sua aspettativa di vita, decise di alzare gli occhi e di dedicarsi alle cose delle stelle.

Lo fece scrutando dentro di sé l’inesauribile Universo che aveva nel suo cuore. Credo che in quel momento, e nei molti di grande sofferenza fisica che ha dovuto inevitabilmente affrontare in tutta la sua vita, lo abbia accompagnato l’idea che i sogni sono essenziali allo spirito delle grandi imprese. Lui ne aveva uno grande: voleva fortemente la laurea in cosmologia all’Università di Cambridge, voleva andare dentro il Big Bang e scrivere le equazioni delle origini dell’Universo.
Lo fece partendo da Oxford, la città dalle sognanti guglie – lì dove anche i campanili si stagliano a guardare le stelle – dove lui era nato nel 1942 al riparo dal grigio cielo di metallo dei bombardieri e dei bombardamenti, perché rispetto a Londra – come scriverà nell’incipit di Buchi neri e universi neonati. Riflessioni sull'origine e il futuro del cosmo – quello «era un posto più favorevole in cui nascere durante la seconda guerra mondiale: c’era infatti un accordo per cui i tedeschi non avrebbero bombardato Oxford e Cambridge e gli inglesi avrebbero analogamente risparmiato dalle bombe Heidelberg e Göttingen», aggiungendo «è un peccato che un accordo così civile non sia stato esteso anche ad altre città».

Ma il Professor Hawking, lui lo aveva scritto nel suo nome, era destinato a Cambridge, lui era destinato alla prestigiosissima cattedra lucasiana del King’s College, la stessa che fu di Sir Isaac Newton, di cui fu reggente per 30 anni, dal 1979 al 2009.

Ci arrivò studiando per primo le singolarità gravitazionali, andando oltre e poi ben oltre l’orizzonte degli eventi che la sua malattia gli aveva prospettato. Lo ha fatto con la tenacia e la dedizione di chi, anche se costretto all’immobilità su una sedia a rotelle, non smise mai di credere che c’è sempre qualcosa che è possibile fare. E lui non smise mai di dedicarsi allo studio teorico dei misteri del Cosmo, cercando continuamente la via di coniugazione tra la relatività generale e la meccanica quantistica, tra la perfetta simmetria del principio cosmologico e ogni possibile implicazione di quello antropico, fino alle moderne congetture del multiverso e dell’inflazione caotica dell’universo.

Lui che contro ogni stima ha vissuto ben altri 55 anni oltre quel lontano breve orizzonte del 1963, lui che prima di tutti si è immerso nel mistero dei buchi neri.

E che dalle loro oscurità profondissime ha tirato fuori la possibilità che da loro si possa ‘fisicamente’ fuggire, evaporando, per mezzo di una radiazione che porta il suo nome, e che potrebbe essere contenuta nella radiazione di fondo dell’Universo; lui che ha svelato all’uomo la grandezza delle stelle e alle stelle la grandezza dell’uomo, la grandezza di sé, del suo sogno di scienziato e di matematico e della forza vitale straordinaria con cui ha realizzato ogni cosa, arrivando da un lato fino alle origini del Cosmo e abbattendo con le sue teorie persino i confini sulle origini dell'Universo (è sua la teoria sull'inizio senza confini dell’Universo), e dall’altro demolendo la vergogna - tutta terrestre e terrena - che a volte l’uomo mette nelle barriere alle persone diversamente abili.
È stato cosmologo, fisico, matematico, astrofisico, scienziato, fra i più autorevoli e conosciuti fisici teorici al mondo, noto soprattutto per i suoi studi sui buchi neri, sulla cosmologia quantistica e sulle origini dell'universo. Portano il suo nome la radiazione di Hawking, lo stato di Hartle-Hawking, noto anche come Teoria dello stato senza confini, e l’asteroide di fascia principale 7672 Hawking. 

Eccellente divulgatore e chiarissimo comunicatore, nonostante la malattia ne abbia condizionato la forma del linguaggio a quello di un sintetizzatore vocale.

«Mente da genio e voce da robot, non potrebbe esserci miglior amico di lui» diranno del Professor Hawking i protagonisti della sitcom The Big Bang Theory. Ha conservato fino alla morte il titolo di direttore del Dipartimento di Matematica Applicata e Fisica Teorica dell’Università Cambridge, e non è un caso che lui sia volato alle stelle e alla sua radiazione cosmica proprio la mattina del 14 marzo, il giorno dedicato all'irrazionale e trascendente Pi Greco, pilastro di tutta la matematica e "stella miliare" [ndr] di tutti gli Universi, oltre ad essere il giorno in cui 139 prima è nato Albert Einstein.

Leggi anche Stefania Bergo | Pi greco: il numero delle meraviglie che governa l'universo

In lui ha abitato un sogno talmente grande, e una forza dentro di sé gigantesca per realizzarlo, che alla fine ne ha contenuti un’infinità di sogni: un "multiverso" di sogni e di stelle.

Hawking è stato energia vitale oltre la materia del suo corpo. Lui è stato tante cose, ma prima di tutto è stato un uomo eccezionale. Lui sì, è stato fatto "della stessa sostanza dei sogni" e della stessa materia delle stelle. Ed a quella è tornato.

Vogliamo comprendere ciò che vediamo attorno a noi e chiederci: Qual è la natura dell'Universo? Qual è il nostro posto in esso? Da che cosa ha avuto origine l'universo e da dove veniamo noi? [...] quand'anche ci fosse una sola teoria unificata possibile, essa sarebbe solo un insieme di regole e di equazioni. Che cos'è che infonde vita nelle equazioni e che costruisce un universo che possa essere descritto da esse? L'approccio consueto della scienza, consistente nel costruire un modello matematico, non può rispondere alle domande del perché dovrebbe esserci un universo reale descrivibile da quel modello. Perché l'universo si dà la pena di esistere? [...] Se però perverremo a scoprire una teoria completa, essa dovrebbe essere col tempo comprensibile a tutti nei suoi principi generali, e non solo a pochi scienziati. Noi tutti – filosofi, scienziati e gente comune – dovremmo allora essere in grado di partecipare alla discussione del problema del perché noi e l'universo esistiamo. Se riusciremo a trovare la risposta a questa domanda, decreteremo il trionfo definitivo della ragione umana: giacché allora conosceremmo la mente di Dio.
Stephen Hawking

«Viviamo in un mondo che ci disorienta con la sua complessità»

Se un giorno verrà compiuta e provata questa Teoria del Tutto – anche se a me piace più chiamarla con il suo nome inglese, Theory Of Everything (TOE), perché mi sembra che “Everything” includa ancora più cose che “Tutto” – allora avremo raccolto un’altra enorme eredità, l’eredità di un genio che ha raccolto su di sé quella di tre secoli di pensiero scientifico moderno per volare via il giorno di π e del compleanno dello zio Albert.
Ma forse, il 14 marzo 2018, da qualche parte del mondo è nato il bambino, o la bambina (speriamo che sia femmina), che prenderà questa eredità e completerà la TOE.

Il Cosmo non è gran cosa se dentro non ci sono le persone che ami.
Stephen Hawking

Vincenzo Mirra Nato a Napoli nel 1973, si è diplomato all'Istituto Nautico per poi laurearsi in Ingegneria Aeronautica ad indirizzo Spaziale. Alle passioni per la navigazione, il mare e l’astronautica, ha sempre aggiunto quelle per la letteratura, la scrittura di viaggio e di meditazione ed il teatro. È autore del blog letterario Beaufort, scritture al vento e taccuini di mare che esprime scritture di vario tipo e argomentazione, anche di natura sperimentale. Dal 2005 vive a Pisa, dove dal 2015 ha iniziato a frequentare corsi e laboratori teatrali, di recitazione, di lettura corale e di drammaturgia. Isole, AUGH! Edizioni. I MIEI ARTICOLI

Leggi >

L'Universo: diario di bordo del capitano

Scienza | Di Vincenzo Mirra. Backstage della Navigazione siderale: diario di bordo del capitano, l'ultima puntata di un emozionante viaggio alla scoperta dell'universo.

stelle riemergono
dall’abisso
del tempo siderale,
lampare celesti
di sogni
e segreti,
notturne promesse
(da una mia poesia, contenuta nella raccolta Isole)

Bisogna avere un caos dentro di sé, per generare una stella danzante.
(Nietzsche)

Nel caso dell’ultima osservazione GW170817 (17 agosto 2017) le stelle danzanti erano due. Due stelle di neutroni nella galassia di Herschel NGC 4993, nella costellazione dell’Hydra.

Per la cronaca astrofisica, GW170817 è stato il quinto segnale gravitazionale rilevato ed il primo chirp cosmico associato alla collisione tra stelle di neutroni. 

Dirò un’altra cosa a proposito delle stelle. Le stelle danzano. 

E quelle di neutroni, per effetto di un campo magnetico intensissimo, danzano in modo frenetico come stelle pulsanti (pulsar). Una volta per quanto veloce e regolare fossero le loro intermittenze, queste pulsar erano chiamate LGM, come acronimo di Little Green Men - piccoli omini verdi -, perché qualcuno pensò che potessero essere potenti segnali trasmessi da una qualche forma di vita extraterrestre.

Queste le tappe principali del viaggio di esplorazione che abbiamo iniziato a navigare nell’oceano siderale dello spazio-tempo:

Dei buchi neri e di altre stelle (o quasi stelle) dell'universo: tutte le puntate

Scienza Leggi altri articoli Scienza

E questa la lista di onde gravitazionali osservate sperimentalmente di cui vi ho parlato nel corso delle puntate ( vai alla lista di GW completa e aggiornata di tutti gli eventi):

• 2015, 14 settembre (GW150914): prima osservazione di onde gravitazionali da parte degli osservatori americani dei centri LIGO.
• 2016, 14 febbraio: annuncio da parte della collaborazione scientifica congiunta LIGO e EGO-Virgo della scoperta delle onde gravitazionali relativa alla prima osservazione Gli scrittori della porta accanto - Dalla relatività di Einstein alle onde gravitazionali.
• 2017: nel mese di febbraio avviene l’inaugurazione di Advanced Virgo, ed il 1 agosto Virgo si unisce a LIGO nell’ascolto di sorgenti dall’oceano siderale per una presa dati di quattro settimane. Mai scelta del tempo è mai stata più propizia. Agosto sarà un mese eccezionale.
• 2017, 14 agosto (GW170814): gli interferometri gravitazionali rilevano la collisione di due buchi neri avvenuta nella costellazione di Eridano, nell’emisfero celeste australe, 1,8 miliardi di anni prima. Per la prima volta anche le antenne Virgo catturano le oscillazioni dell’universo che vibra della collisione di due buchi neri dalle profondità cosmiche di 1,8 miliardi di anni luce. GW170814 è il quarto segnale gravitazionale rilevato ed è il primo evento cosmico registrato simultaneamente da tutti gli interferometri in ascolto gravitazionale, i due americani di LIGO, e l’interferometro VIRGO che si trova a Pisa, a venti minuti (non di luce ma di macchina) da dove abito io.
• 2017, 17 agosto (GW170817): tre giorni dopo la prima rilevazione simultanea LIGO-Virgo, tutti i centri di osservazione planetaria rilevano il primo evento gravitazionale relativo alla collisione di due stelle di neutroni; l’onda gravitazionale GW170817 è rilevata dagli interferometri LIGO e Virgo, mentre il lampo gamma di coalescenza GRB170817A è osservato dai telescopi spaziali orbitanti NASA-Fermi e ESA-INTEGRAL.
• 2017, 27 settembre: annuncio della prima rivelazione congiunta LIGO e EGO-Virgo di onde gravitazionali relativa all’evento GW170814, rilevato il 14 agosto 2017 ed analizzato con l’uso combinato dei dati di Advanced Virgo e di quelli dei due osservatori di Advanced LIGO.
• 2017, 3 ottobre: annuncio del premio Nobel per la fisica agli scopritori delle onde gravitazionali.
• Il premio Nobel per la fisica va ai padri dell’esperimento americano LIGO, ma è un riconoscimento meraviglioso per tutta la collaborazione interazionale LIGO-Virgo ed è una soddisfazione enorme per tutti i ricercatori e gli scienziati che lavorano con passione e dedizione all’esperimento congiunto. Ne conosco alcuni. Sono tutti sognatori e cacciatori di stelle, sì, anche di quelle nere densissime. Sanno cogliere la bellezza ovunque, sì, anche nei numeri di interferometria e nelle forme d’onda. Come lo spazio-tempo oscilla di onde gravitazionali, così questo premio Nobel oscilla di bellezza.
• 2017, 16 ottobre: annuncio della prima rilevazione di onde gravitazionali relativa alla collisione di un sistema binario di stelle di neutroni (eventi GW170817, onda gravitazionale, e GRB170817A, lampo gamma)

Editoriali Leggi altri articoli di Vincenzo Mirra

Vincenzo Mirra Nato a Napoli nel 1973, si è diplomato all'Istituto Nautico per poi laurearsi in Ingegneria Aeronautica ad indirizzo Spaziale. Alle passioni per la navigazione, il mare e l’astronautica, ha sempre aggiunto quelle per la letteratura, la scrittura di viaggio e di meditazione ed il teatro. È autore del blog letterario Beaufort, scritture al vento e taccuini di mare che esprime scritture di vario tipo e argomentazione, anche di natura sperimentale. Dal 2005 vive a Pisa, dove dal 2015 ha iniziato a frequentare corsi e laboratori teatrali, di recitazione, di lettura corale e di drammaturgia. Isole, AUGH! Edizioni. I MIEI ARTICOLI

Leggi >